Theorem
Let \(f_1(x)\), \(f_2(x)\), and \(g(x)\) be functions of \(x\) over the real interval \(X\equiv[A,B]\). Also let \(x_1,x_2\in[A,B]\). If:

For all \(x\in[0,B]\), \(f_2(x) \geq f_1(x)\),
\(f_1(x)\) is increasing, \(g(x)\) is continuous,
\(f_2(A) \geq f_1(A) > g(A)\),
For each \(i\), and \(\forall x \in X, f_i(x)=g(x)\Leftrightarrow x=x_i\),

Then \(x_2\geq x_1\)

Proof

If \(x < x_1\), then \(f_1(x)>g(x)\).
Let \(\dot{x} \equiv \inf \left\{ x\in X \mid f_1(x) \leq g(x) \right\} \).
If \(x < \dot{x}\), then \(f_1(x)>g(x)\) .
It must be that \(\dot{x}=x_1\).
Note that \(\dot{x} > A\)
By the continuity of \(g(x)\), there is an \(\varepsilon > 0\) such that \(g(x)< f_1(A)\) for all \(x \leq A+\varepsilon\).
But \(f_1 \) is increasing, so for all \(x\leq A+\varepsilon\), \(f_1(x)\geq f_1(A)\).
Thus for all \(x\leq A+\varepsilon\), \(f_1(x) > g(x)\). So \(\dot{x} \geq A+\varepsilon\).
Note that if \(x < \dot{x}\), then \(f_1(\dot{x})\geq f_1(x) > g(x)\).
The set of \(x<\dot{x}\) is nonempty, so by the continuity of \(g(x)\), \(f_1(\dot{x})\geq g(\dot{x})\).
If \(f_1(\dot{x})> g(\dot{x})\), then a contradiction arises:
By the continuity of \(g(x)\), there is an \(\varepsilon > 0\) such that \( f_1(\dot{x}) > g(x)\) for all \(x\in B_\varepsilon [\dot{x}]\).
But \(f_1 \) is increasing, so for all \(x\geq\dot{x}\), \(f_1(x)\geq f_1(\dot{x})\).
Thus for all \(x\leq \dot{x}+\varepsilon\), \(f_1(x)\geq f_1(\dot{x}) > g(x)\).
And so \(\dot{x}\) is not the infimum of \(\left\{ x\in X \mid f_1(x) \leq g(x) \right\}\). ↯.
Therefore \(f_1(\dot{x})=g(\dot{x})\), which implies that \(\dot{x}=x_1\).
So if \(x < x_1\) then \(f_2(x)\geq f_1(x) > g(x)\).
And \(f_2(x_2)=g(x_2)\), so by contrapositive, \(x_2 \geq x_1\).

But also, I mean, just look at it.

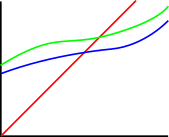
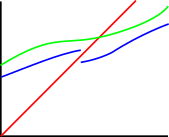
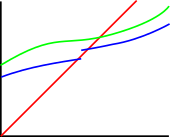
If you shine a beam (\(g\)) up at two continuous barriers, and one barrier (\(f_1\)) is always on top of the other (\(f_2\)), then the beam will strike the barrier on the bottom first.
To strike the top barrier first, the beam has to make it through a gap in the bottom barrier without striking it. This kind of gap doesn't work because \(f_1\) is increasing.
And this kind of gap doesn't work because to fly through it, the beam would have to travel to the left, which it can't do because it's a continuous function of \(x\). Even if we wiggle the beam a bit, it can't go left. So even if we allow for discontinuities, the beam can't get through.