McCall Job Search
A One-sided Search Model of Employment
Here, we model a person looking for a job. This person gets random job offers which they can choose to accept or reject.
Details of the Model
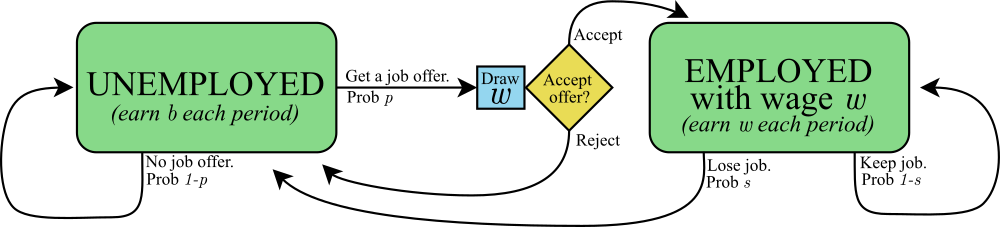
In this model, a person is either employed or unemployed.
- If they are unemployed, then:
- They receive some unemployment benefit $b$,
- and they search for a job:
- There is some probability $p$ that they get a job offer.
- If they do get a job offer, then this offer has a randomly-drawn wage $w$
- They can choose to accept the job, or reject the job (which means they will still be unemployed tomorrow).
- If they are employed in a job with wage $w$, then:
- They earn that wage $w$,
- and then there is a random chance $s$ that they lose their job.
The Reservation Wage
When should the person accept an offer with wage $w$? Only when the offered wage is high enough to be ‘worth it’.
The Reservation Wage, labelled $w^\ast$, is the lowest wage which the person is willing to accept.
Label the value1 of being unemployed as $V_u$, and the value of being employed with wage $w$ as $V_e(w)$. Then:
\[V_e(w^\ast) = V_u\]The person will accept a job offer only if $w \geq w^\ast$, and the probability that they accept a random offer $w$ is therefore $\Pr(w \geq w^\ast)$
Steady-state Unemployment Rate
Let’s simplify the above picture by noting the transition probabilities:
- There is a probability $s$ that an employed person becomes unemployed.
- There is a probability $p \cdot \Pr(w \geq w^\ast)$ that an unemployed person becomes employed.
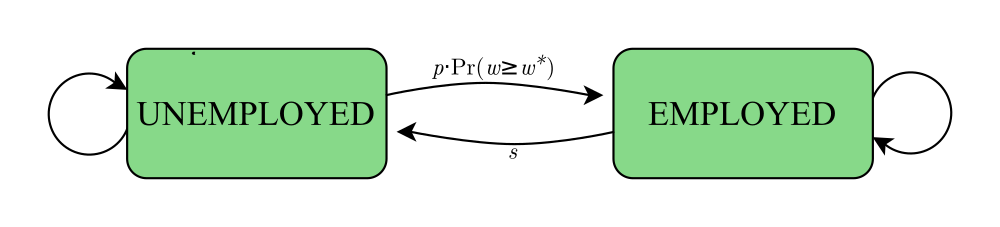
Let $U$ be the percentage of people who are unemployed, and $1-U$ the percentage employed. Then for the flows between these two categories to be equal, it must be that:
\[\textcolor{#6c71c4}{(1-U)} \cdot \textcolor{#268bd2}{s} = \textcolor{#dc322f}{U} \cdot \textcolor{#b58900}{p \cdot \Pr(w \geq w^\ast)}\]The amount of employed people who lose their job equals the amount of unemployed people who start a new job.
Solving for $U$, we find the steady-state unemployment rate is
\[U = \frac{s}{s+p\cdot\Pr(w \geq w^\ast)}\]Other Search Models
Many other variants of search and matching models exist.
For example, one can build a Two-sided model of search, where unemployed workers are looking for jobs, and where firms are looking for workers to fill vacant positions.
These kinds of two-sided search models are concerned not just with the unemployment rate, but also the vacancy rate, which is the portion of job positions which currently lack a worker filling them. (The BLS also uses the term “job openings rate”. This is synonymous with “vacancy rate”.)
Links
- Some Graphs from the BLS’ Job Openings and Labor Turnover Survey:
- Hires and Seperations rates
- A curve plotting Unemployment Rates vs Vacancy Rates (aka “The Beveridge Curve”)
-
An agent’s “value function” is related to but slightly different from their utility function. For now, you can think of the value function like “expected utility, taking into account all the possible things that could happen in the future, and assuming that your future self makes optimal decisions.” ↩